Cracking the Code of Math: How Python Makes Complex Symbols Simple
Ever felt like math homework was a secret code written in Greek and weird squiggly lines? We’ve all been there. Symbols like ∑ (summation), n! (factorial), and those intimidating matrices often feel abstract, but guess what? When you look at them through the lens of Python, they become simple, executable commands.
You don’t need to be a math genius or a senior developer to bridge this gap. You just need your favorite programming language and two key libraries: NumPy for number crunching, and SymPy for the pure symbolic algebra.
Let’s stop just reading the math and start doing the math!
1. ∑ Summation: Adding Up Everything (and More!)
The Sigma (∑) is the rock star of mathematical symbols. It just means “add it all up.” Whether you’re dealing with statistics, calculus, or data science, you’ll encounter it.

It’s essentially a fancy loop! It tells you to loop from a starting point (i=1) to an ending point (n) and apply the function inside.
The Pythonic Way (Numerical)
For simple, finite series, the built-in Python sum() function combined with a generator expression or range() is the cleanest solution.
Python
# Let's calculate the sum of the squares of the first 5 integers: 1² + 2² + 3² + 4² + 5²
upper_limit = 5
numerical_sum = sum(i**2 for i in range(1, upper_limit + 1))
print(f"The total sum is: {numerical_sum}")
# Output: The total sum is: 55 (1 + 4 + 9 + 16 + 25)
The SymPy Way (Symbolic)
What if you don’t want a final number? What if you want the formula itself, which you can then plug any number into? That’s when SymPy becomes your superhero.
Python
from sympy import summation, symbols
# Define 'i' as our looping variable and 'n' as the symbolic upper limit
i, n = symbols('i n')
# Calculate the symbolic sum of i^2 from i=1 to n
expression = summation(i**2, (i, 1, n))
print(f"The General Formula is: {expression}")
# Output: The General Formula is: n*(n/2 + 1/2)*(n + 1)/3
# Now, we can easily evaluate this formula for n=100
result_for_100 = expression.subs(n, 100)
print(f"The sum when n=100 is: {result_for_100}")
# Output: The sum when n=100 is: 338350
Takeaway: Python’s flexibility lets you choose: numerical output with sum(), or the exact, elegant formula with SymPy.
2. n! Factorial: The Power of math
The factorial (n!) is simpler but grows incredibly fast. It’s just multiplying a number by every positive integer below it.
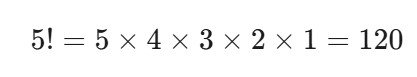
Factorials are vital in probability, permutations, and series expansions.
Direct Calculation is Trivial
The standard Python math library has a function ready to go, so you never have to write a loop for this again.
Python
import math
n = 7 # We want to calculate 7!
result = math.factorial(n)
print(f"The factorial of {n} is: {result}")
# Output: The factorial of 7 is: 5040
Combining Symbols: Sum of Factorials
Let’s use our new skills to compute a more complex expression, like the sum of the first four factorials: 1!+2!+3!+4!.
Python
import math
# Use a generator expression inside sum() to calculate and add up the values
sum_of_factorials = sum(math.factorial(k) for k in range(1, 5))
print(f"1! + 2! + 3! + 4! = {sum_of_factorials}")
# Output: 1! + 2! + 3! + 4! = 33
That was incredibly clean, right? No verbose loops, just beautiful, functional Python.
3. A Matrices: Linear Algebra with NumPy
If you’ve ever dealt with data analysis, machine learning, or 3D graphics, you’ve dealt with matrices. They are just grids of numbers that let us solve huge systems of equations efficiently.
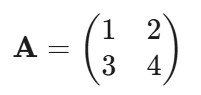
NumPy is the industry standard for this. When you hear “matrix” in Python, you should think numpy.array.
Matrix Multiplication (The Right Way)
Matrix operations, like multiplication, follow very specific rules. Python and NumPy make these complicated rules easy.
Python
import numpy as np
A = np.array([[1, 2],
[3, 4]])
B = np.array([[5, 6],
[7, 8]])
# Element-wise multiplication (NOT matrix multiplication)
C_element = A * B
# True Matrix Multiplication (Dot Product)
C_dot = A @ B # Use the elegant '@' operator (Python 3.5+)
print("Element-wise Multiplication (A * B):")
print(C_element)
# Output: [[ 5 12] [21 32]]
print("\nTrue Matrix Multiplication (A @ B):")
print(C_dot)
# Output: [[19 22] [43 50]]
Pro Tip: Always use the @ operator for true matrix multiplication. Using * does simple element-by-element multiplication, which is usually not what you want in linear algebra!
The Big Guns: Inverse and Determinant
Two of the most common and powerful operations are finding the determinant (a single number that tells us a lot about the matrix) and the inverse (used to ‘undo’ a matrix operation). NumPy makes both trivial.
Python
from numpy import linalg as la
# Matrix A: [[1, 2], [3, 4]]
# Get the determinant
det_A = la.det(A)
# Get the inverse matrix
inv_A = la.inv(A)
print(f"\nDeterminant of A: {det_A:.2f}")
# Output: Determinant of A: -2.00
print("\nInverse Matrix of A:")
print(inv_A)
# Output:
# [[-2. 1. ]
# [ 1.5 -0.5]]
The Final Equation: Code = Clarity
We just took three of the most common and often confusing mathematical symbols and broke them down into simple, three-line Python scripts.
| Math Symbol | Concept | Python Library | Core Command |
| ∑ | Summation | sum() or SymPy | sum(iterable) / summation() |
| n! | Factorial | math | math.factorial() |
| A | Matrix/Array | NumPy | np.array() / @ / linalg.inv() |
Python truly is the universal translator for mathematics. It takes the abstraction of symbols and turns it into tangible, verifiable code. Now that you’ve got the tools for summation, factorials, and matrices, what complex mathematical concept are you going to conquer next?
Ready to master more mathematical symbols with code? Dive deeper with these related posts:
- Understanding Calculus with Python: Learn how to tackle derivatives (dxd) and integrals (∫)!
- Solving Linear Equations with NumPy: See how to find solutions to systems of equations using matrix methods!
Let me know in the comments what other symbols or math topics you want to see simplified!